2024 노벨 물리학상과 머신러닝의 관계


For foundational discoveries and inventions that enable machine learning with artificial neural networks — The Nobel Prize in Physics 2024


물리학에 이어 화학까지—2024년 노벨상과 AI
매년 10월이 되면 월요일부터 한 주 동안 생리의학, 물리학, 화학, 문학, 평화, 경제학 분야의 노벨상이 발표됩니다[1]. 올해에도 10월 7일 생리의학상 발표를 시작으로 수상자들이 공개되었습니다. 8일 물리학상, 9일 화학상 수상자 발표는 학계에 큰 반향을 일으켰는데, 그 이유는 물리학상 수상자로 현 AI 시대에 지대한 영향을 미친 두 학자, John Hopfield(프린스턴 대학)와 Geoffrey Hinton(토론토 대학)이 선정되고, 이어 화학상 수상자로 단백질 구조 예측 AI를 개발한 David Baker(워싱턴 대학), Demis Hassabis(Google DeepMind), John Jumper(Google DeepMind)가 발표되었기 때문입니다. 이는 지금이 AI 시대임을 여실히 보여주는 수상 결정이었습니다.
수상자 발표 후 많은 이들이 찬사와 인정을 보였으나, 일부는 회의적인 시각을 보이기도 했습니다. 화학상의 경우, 수상자들이 개발한 RoseTTAFold와 AlphaFold의 개발이 화학 분야에 큰 변화를 가져왔기 때문에 많은 이들이 수상에 공감하고 있습니다. 반면, 물리학상 수상은 "AI가 물리?"라는 의구심을 자아냈습니다. 그러나 energy-based model과 같은 AI 이론을 학습한 사람이라면, Hopfield와 Hinton의 수상 소식에 쉽게 박수를 보낼 수 있을 것입니다.
Hopfield와 Hinton은 AI 분야에서 어떤 연구를 해왔을까요? 또 그들의 연구는 물리학과 어떤 관계가 있었을까요? 이번 글에서 자세히 알아보겠습니다.
2024 노벨 화학상 수상을 가능하게 한 AlphaFold 2에 대해 더 알아보세요:
Hopfield network (홉필드 네트워크)—연상 기억의 원리를 모델링한 인공신경망
물리학자였던 John Hopfield는 1970년대에 이미 생물물리학 분야에 지대한 영향을 주는 인물이었습니다 [PNAS 1974] [Google Scholar]. 당시 생물물리학 분야의 다른 학자들처럼 Hopfield 또한 우리의 뇌가 작동하는 원리에 대해 궁리하였습니다. Hopfield의 관련 연구들 중 이번 노벨상이 주목한 그의 성과는 바로 Hopfield network입니다.
Hopfield network [PNAS 1982]는 연상 기억 (associative memory)의 원리를 모델링한 인공신경망입니다. 인공신경망을 이용한 딥러닝에는 이미 많은 분들이 익숙하실 텐데요, Hopfield network는 요즘 쓰이는 일반적인 인공신경망 모델과는 용도가 조금 다릅니다. 처음 보는 분자의 물성을 맞추거나 새로운 분자 구조를 만들어내는 예측·생성의 역할 대신, 여러 정보들 (데이터들)을 기억한 후 해당 정보들을 나중에 검색할 수 있게 해줍니다. 마치 컴퓨터의 디스크 드라이브와 비슷하죠.
하지만 디스크 드라이브와 Hopfield network는 큰 차이가 있습니다. 디스크 드라이브처럼 정보가 저장되어 있는 주소를 사용해 정보에 접근하는 대신, Hopfield network는 정보에 대한 대강의 내용을 입력받으면 완전한 정보로 정제하여 건네줍니다(content-addressable memory). 즉, 연상 기억의 기능을 수행하죠. 아래의 그림으로 Hopfield network의 기능을 더 명확하게 이해할 수 있습니다.

Hopfield network의 원리: 스핀 유리를 이용한 인공 기억의 구현
Hopfield network의 흥미로운 점은 기능보다는 그 원리에 있습니다. Hopfield network는 아주 단순한 연산만 하는 단위들(units, nodes 또는 neurons)이 집단을 이루어, 하나의 네트워크가 여러 가지 패턴을 기억할 수 있는 창발성(emergence)을 나타냅니다. Hopfield는 이러한 네트워크를 고안하기 위해, 응집물리학에서 물질의 자성을 모사하는 대표적인 이론인 스핀 유리(spin glass) 이론을 빌렸습니다.
Hopfield network는 아래 그림처럼 \(N\)개의 뉴런들로 구성됩니다. 뉴런 \(i\)는 그것의 값 \(V_i\), 즉 활성 상태로 \(1\) (뉴런이 켜짐)과 \(-1\) (뉴런이 꺼짐) 중 하나를 가집니다 [3]. 또한, 모든 뉴런들은 서로가 서로와 연결되어 있고, 뉴런 \(i\)와 뉴런 \(j\) 사이의 연결은 가중치 \(w_{ij}\)로 묘사됩니다 (단, \(\forall i\ w_{ii}=0\); \(\forall i\forall j\ w_{ij}=w_{ji}\)).
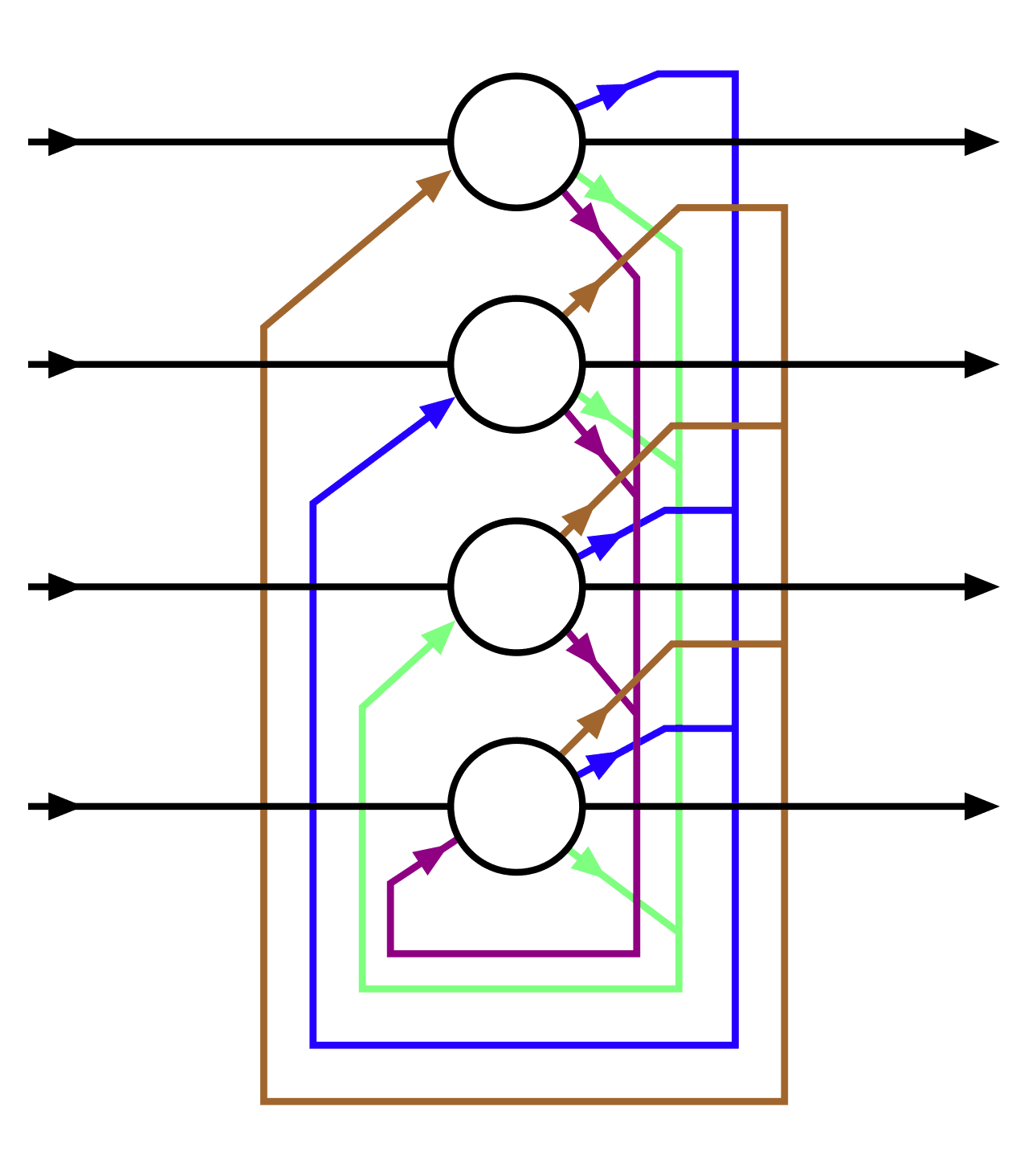
최초 입력과 최종 출력을 나타내고, 그 외 색깔 화살표들은
노드 간의 연결을 나타내며 각각 가중치를 지닌다 [Wikipedia].
Hopfield network가 작동하기 위해선 우선 데이터들을 기억, 즉 학습해야 합니다. Hopfield network의 학습은 일반적인 딥러닝 모델의 학습에 비해 매우 간단합니다. 각 데이터 \(\mathbf{x}^{(k)}\)가 \(N\)개 뉴런의 활성 상태로 표현될 때 (즉, 길이 \(N\)의 이진 벡터로 표현될 때), \(p\) 개의 데이터를 학습하기 위해서는 다음 식에 따라 뉴런 간 가중치를 부여하면 됩니다:
\[ w_{ij} = \frac{1}{p}\sum_{k=1}^p x^{(k)}_i x^{(k)}_j. \]
가중치가 뉴런들의 상관 (correlation)으로 표현된 것을 알 수 있습니다. 이러한 가중치의 정의는 “neurons that fire together, wire together”로 요약되는 Donald Hebb의 학습 이론을 따릅니다.
학습이 끝난, 즉 가중치들이 모두 정해진 Hopfield network를 사용할 때에는 다음의 알고리즘을 따릅니다:
- 저장된 데이터 중 하나를 불완전하게 묘사하는 값들로 뉴런들을 초기화한다.
- 무작위 순서로 뉴런들의 값을 다음에 따라 업데이트 한다:
\[ V_i \leftarrow \begin{cases} +1 &\text{if } \sum_j w_{ij}V_j \ge \theta_i, \\ -1 &\text{otherwise}. \end{cases} \]
이 때, \(\theta_i\)는 뉴런 \(i\)의 역치 (threshold)를 표현하며, 보통 \(0\)으로 지정한다. - 뉴런들에 더 이상의 업데이트가 없을 때까지 위 2를 반복한다.
Hopfield network의 용량이 충분했다면, 위 알고리즘이 끝난 뒤에는 네트워크가 학습했던 데이터들 중 입력으로 주어진 정보에 가장 가까운 데이터로 수렴하게 됩니다. 바로 content addressing을 하는 것이죠.
지금 절의 초반에 스핀 유리 얘기를 했었지요. Hopfield network의 물리적 원리는 위 알고리즘의 에너지적 관점에서 살펴볼 수 있습니다. Hopfield network의 상태는 다음과 같은 에너지로 나타낼 수 있습니다:
\[ E = -\frac{1}{2}\sum_{i,j}w_{ij}V_iV_j + \sum_i\theta_iV_i. \]
이 식은 스핀 유리 시스템의 총 에너지를 나타내는 물리식과 일치합니다. 또한, 알고리즘에서 뉴런을 업데이트하는 과정은 네트워크 에너지를 점진적으로 줄이며 국소 최솟값 (local minima)에 도달하는 과정과 유사합니다. 가중치가 정해진 Hopfield network는 뉴런들의 값에 따라 하나의 energy landscape을 그리며, landscape에서 각 골짜기, 즉 국소 최저 에너지 지점들은 네트워크가 학습했던 패턴들에 해당합니다.
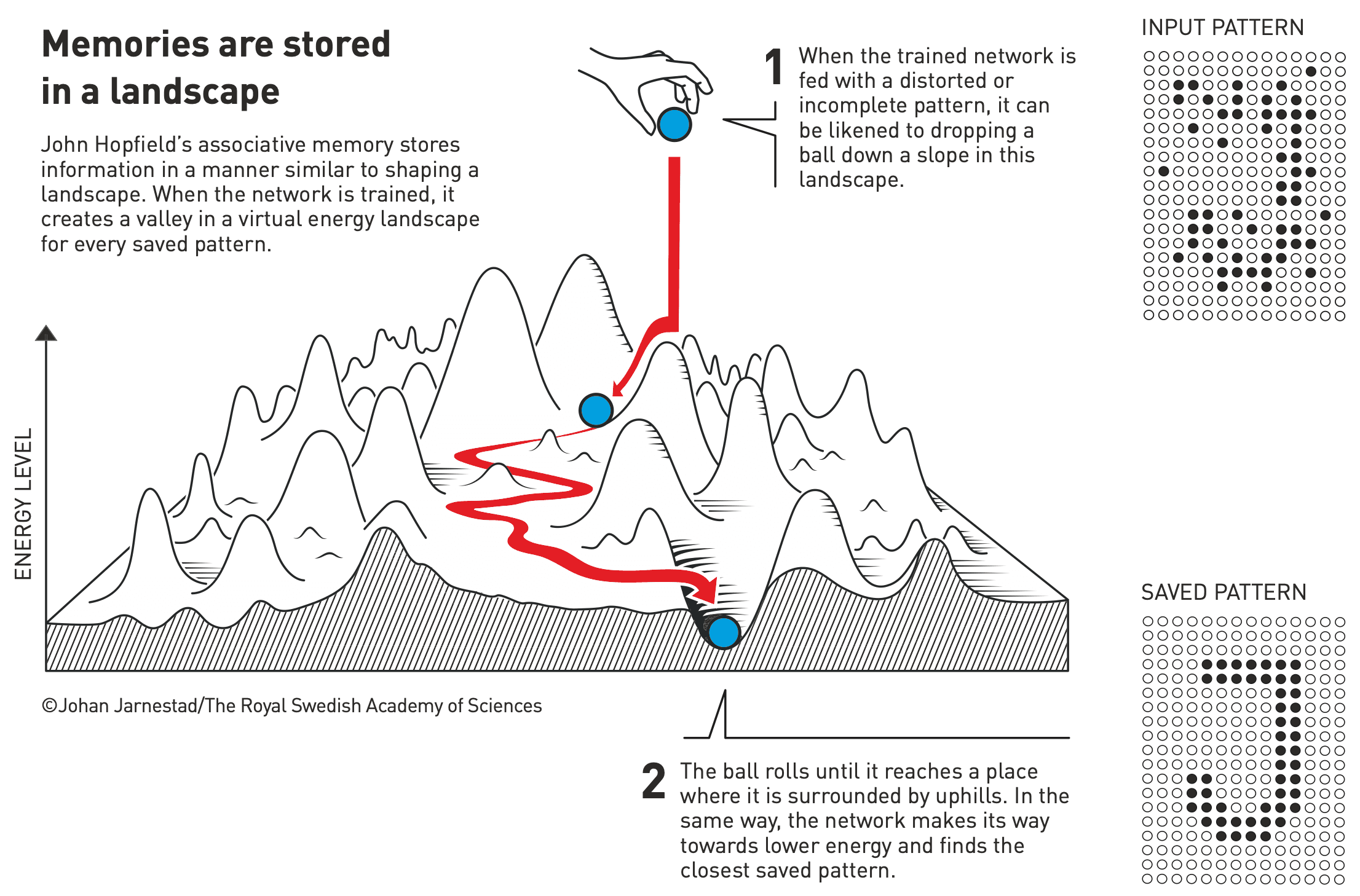
정말 흥미롭지 않나요? 다시 말해 Hopfield는 응집체물리학의 이론과 뇌의 학습 원리에 대한 이론을 이용해 content-addressable memory 모델을 제안한 것입니다.
Restricted Boltzmann machine (RBM)
노벨상을 수상하는 학자들은 일반적으로 오랜 기간 연구를 수행해오고 있는 전문가들이고, 그 덕분에 수상자들은 하나만 꼽을 수 없는 여러 개의 업적을 가지고 있는 경우가 많습니다. AI 연구자와 엔지니어 중 Geoffrey Hinton을 들어보지 못한 사람은 없을 것 같습니다 [Google Scholar]. Yoshua Bengio (몬트리올 대학), Yann LeCun (뉴욕 대학 & Meta)과 함께 딥러닝의 대부라 불리는 Hinton의 대표적인 업적에는 역전파 (backpropagation) [MIT Press 1987], AlexNet [NIPS 2012], dropout [JMLR 2014] 등이 있습니다. 이 같은 대단한 업적들은 그가 2018년에 수상한, 전산학의 노벨상이라 불리는 Turing Award에서도 확인할 수 있습니다.
물론 위 같은 모든 업적들을 모두 기리는 것이겠지만, 이번 노벨상은 Hinton의 restricted Boltzmann machine (RBM)에 대한 성과를 특정했습니다.
Restricted Boltzmann machine의 원리: 현대 딥러닝의 토대
RBM은 Hopfield network보다 더 일반적인 용도로 사용될 수 있는 모델입니다. 별다른 레이블 없이 데이터들을 있는 그대로 관찰하며 데이터들에 내재된 패턴을 학습할 수 있죠 (비지도 학습). 즉 RBM은 지금의 딥러닝 모델들에 더 가까운 모델이며, 실제로 더 직접적인 기반이 되었습니다.
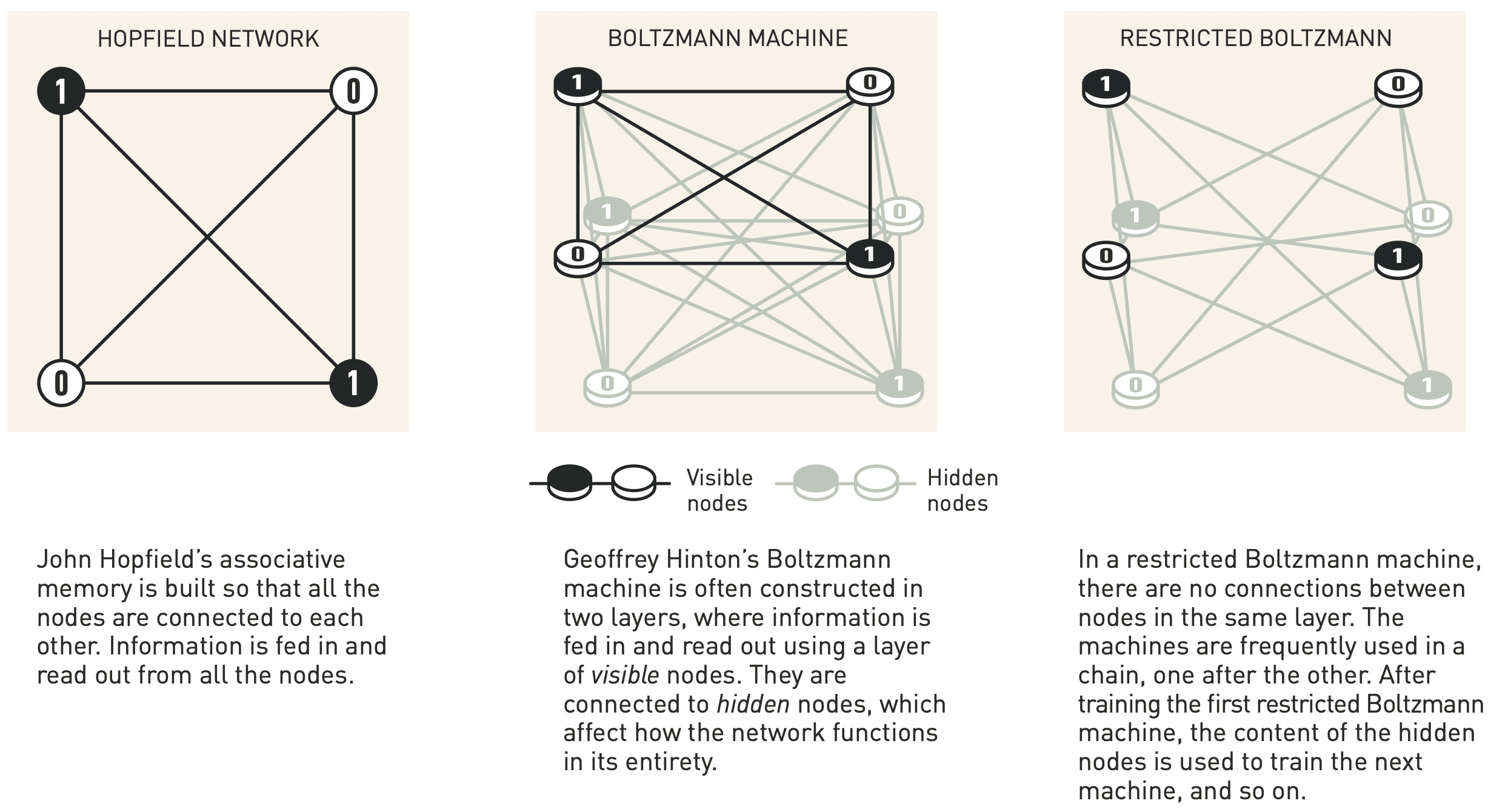
RBM은 Hopfield network와 비슷하게 \(0\), \(1\)의 두 가지 값만 가질 수 있는 뉴런들과 그것들 간의 연결로 구성됩니다. Hopfield network와의 차이점은 (일반적으로) 뉴런들이 가시 (visible) 뉴런 \(v_i\)와 잠재 (hidden) 뉴런 \(h_j\)로 나뉜다는 점입니다. 학습 과정에서 데이터들은 가시 뉴런들에만 입력되고, 잠재 뉴런들은 데이터에 잠재된 패턴을 표현할 수 있도록 학습됩니다.
Hopfield network와 비슷하게, Boltzmann machine에는 가시 뉴런들의 상태 (configuration) \(\mathbf{v}\)와 잠재 뉴런들의 상태 \(\mathbf{h}\), 뉴런들 간 연결의 가중치 \(w_{ij}\)에 따라 다음처럼 에너지가 정의됩니다:
\[ E\left(\mathbf{v},\mathbf{h}\right) = -\sum_{i,j}v_iw_{ij}h_j -\sum_i \theta_iv_i -\sum_j \theta_jh_j. \]
이 역시 스핀 유리 시스템의 에너지를 따릅니다. 또한, Boltzmann machine은 뉴런들의 상태들에 대해 다음처럼 볼츠만 분포에 따른 확률분포를 가지게 됩니다:
\[ P\left(\mathbf{v},\mathbf{h}\right) = \frac{\exp\left[-E\left(\mathbf{v},\mathbf{h}\right)\right]}{\sum_{\mathbf{v},\mathbf{h}} \exp\left[-E\left(\mathbf{v},\mathbf{h}\right)\right]}. \]
데이터들 (\(\mathbf{v}^{(k)}\)들)이 주어질 때, Boltzmann machine의 목표는 학습 데이터들에 대해 높은 확률값을 가지는 확률분포 \(P\)를 배우는 것입니다. 이는 바로 위 Hopfield network에서와 마찬가지로, 학습 데이터들이 국소지점을 이루는 energy landscape \(E\)를 배우는 것과 동일합니다.
학습이 완료된 후 Boltzmann machine은 학습 데이터들과 유사한 새로운 데이터를 생성해낼 수 있습니다. 가시 뉴런들을 적당한 값으로 초기화한 후, 해당 지점으로부터 에너지를 감소시키며 국솟값에 다다르면 그 때의 \(\mathbf{v}\)가 생성된 데이터에 해당하는 것이죠. 초기에 어떤 \(\mathbf{v}\)를 입력했느냐에 따라 생성되는 데이터가 달라지겠죠? 퍼텐셜 에너지 표면을 활보하며 분자 구조를 최적화하거나 샘플하는 원리에 익숙한 분이라면 지금의 설명을 잘 이해할 수 있을 것입니다.
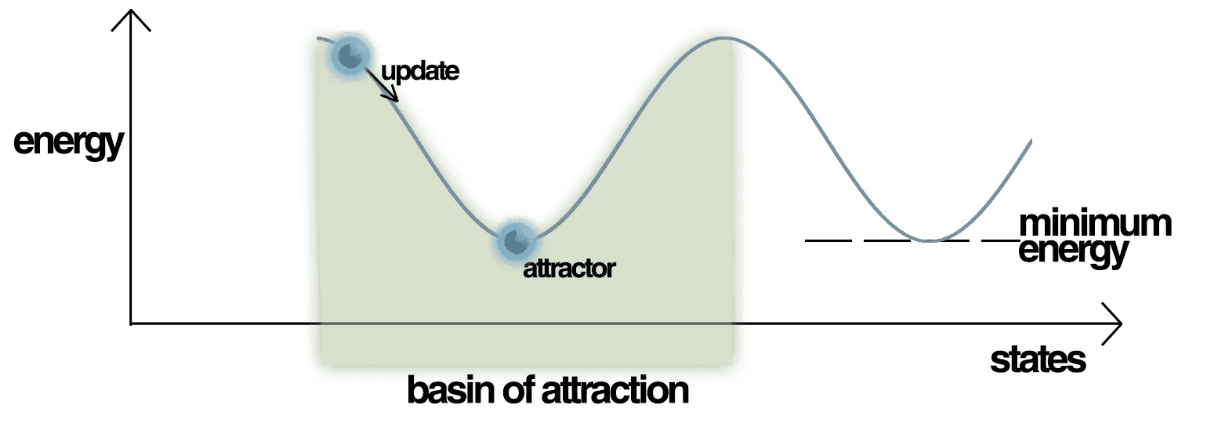
위의 네트워크 비교 그림에서 보듯, 일반적인 Boltzmann machine은 모든 뉴런이 서로 연결되어 있는 반면, RBM은 가시 뉴런끼리나 잠재 뉴런끼리 연결되지 않습니다. 즉, 가시층과 잠재층 안에는 연결이 없고, 가시층과 잠재층 사이만 연결되죠. 이러한 구조적 차이는 Boltzmann machine의 학습을 훨씬 수월하게 만들고, 여러 잠재층을 쌓아 다층 구조, 즉 딥러닝 모델로 확장할 수 있는 기반이 됩니다.
Hinton의 공로—RBM에서 딥러닝까지
Hinton은 동료 학자 Terrence Sejnowski와 함께 1983년, Hopfield network를 기반으로 Boltzmann machine을 제안했습니다 [Cognitive Science Society Conference 1983]. 이처럼 통계물리학적 원리를 접목해, 비지도 학습을 통해 생성 모델로 작동할 수 있도록 만들었죠.
RBM의 경우, 정확히 말하자면 Hinton이 그 창시자는 아닙니다. RBM 자체는 1986년 Paul Smolensky가 제안했죠 [MIT Press 1987]. 반면, Boltzmann이든 RBM이든, 초기에는 학습 시간이 너무 오래 걸려 큰 주목을 받지 못했습니다. 그렇게 한참 시간이 지난 2002년, Hinton이 RBM의 학습을 혁신적으로 가속할 수 있는 contrastive divergence 방법을 제안했습니다 [Neural Computation 2002].
이번 포스트를 너무 복잡하게 만들지 않기 위해, RBM의 학습에 대한 자세한 내용은 생략했습니다만, contrastive divergence는 Boltzmann machine의 학습 중 여러 번 필요한 평형화 (equilibration) 과정의 Gibbs sampling을 간소화시키는 방법입니다.쉽게 말해, 원래 RBM은 학습 데이터 한 예를 처리할 때 매우 많은 연산을 반복해야 했지만, contrastive divergence는 그것을 획기적으로 줄여주면서도 학습의 성능을 충분히 보장했죠.
Hinton은 RBM을 실용화하여, 데이터 생성, 표현 학습, 결측치 보완, 차원 축소, 분류 등 다양한 문제에 활용될 수 있도록 만들었습니다. 또한 이후에 RBM을 다층으로 쌓은 deep belief network를 개발하여 딥러닝 붐의 더욱 직접적인 발판을 마련하였죠 [Neural Computation 2006]. 이 같은 RBM에 대한 연구는 물론, 역전파와 dropout까지 고려하면, Hinton이 왜 딥러닝의 대부로 불리는지 충분히 이해할 수 있습니다.
AI와 물리학의 공생 관계, 그리고 2024년 노벨상
AI가 지금처럼 대성황을 이루기 전, 관심과 연구 투자가 급감했던 몇 차례의 쇠퇴기, 이른바 ‘AI 겨울’이 있었다는 것은 잘 알려진 사실입니다. 1970년대 초, 그리고 1980년대 후반부터 1990년대에 이르기까지, 사람의 사고를 따라 논리와 규칙을 기반으로 AI를 구현하려는 기호주의 (expert system)의 실패 등에 의해 두 번의 큰 겨울을 겪었죠. 그럼에도 Hopfield와 Hinton 같은 학자들은, 이에 반대되는 연결주의(connectionism) 입장에서 연구를 굳건히 이어가며, 오늘날 AI 시대가 열릴 수 있는 기반을 마련했습니다.
앞서 Hopfield network와 Boltzmann machine의 원리를 이해한 독자라면, AI와 물리학이 전혀 무관하다고 보긴 어려울 것입니다. 실제로 두 수상자는 물리학에 적잖은 조예가 있었을 뿐 아니라, 물리학의 개념과 도구를 십분 활용해 뇌의 원리와 인공신경망을 연구했습니다.
올해 노벨 물리학상의 의미는 그 사실만을 기리는 데 그치지 않습니다. AI가 물리학의 힘을 입었을 뿐 아니라, 물리학 또한 AI의 힘을 빌려오고 있습니다 [Popular Information. The Nobel Prize in Physics 2024]. 과거의 노벨 물리학상 수상을 가능케 했던 Higgs 입자의 발견과 중력파의 관측 등에는 AI가 지대한 역할을 수행했습니다. 사실, 이번 노벨 화학상의 주제였던 단백질 구조 예측도 넓게 보면 물리학의 한 분야로 볼 수 있으며, 그 점에서도 물리와 AI가 상부상조한 셈입니다.
업계 종사자 여부를 막론하고, 지금이 AI의 시대임을 부정하는 사람은 드뭅니다. 여기에 더해, 스웨덴 왕립 과학한림원까지 AI의 세계적·사회적 공로를 공식적으로 인정했습니다. 덕분에 AI 분야에는 계속해서 활발한 투자와 연구가 이뤄질 것 같습니다. 히츠는 이번 물리학상과 화학상 수상을 고무적으로 받아들이며, 유용한 AI 기술들을 신약 개발에 접목하고 발전시키기 위해 노력할 것입니다.
[1] 경제학상의 경우 정확한 명칭은 the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel이며, “Nobel Prize in Economics”, 즉 “노벨 경제학상”란 지칭은 부정확하다.
[2] Physics Nobel scooped by machine-learning pioneers [Nature 2024]. 자극적인 제목과 달리 본문은 수상자들이 왜 물리학상을 받을 만한지 점잖게 설명하고 있다.
[3] [PNAS 1982]에서는 \(V_i\in\left\{0,1\right\}\)로 제안되었지만, 수식에 약간의 차이가 생기는 것 외에는 논의가 동일하다.
